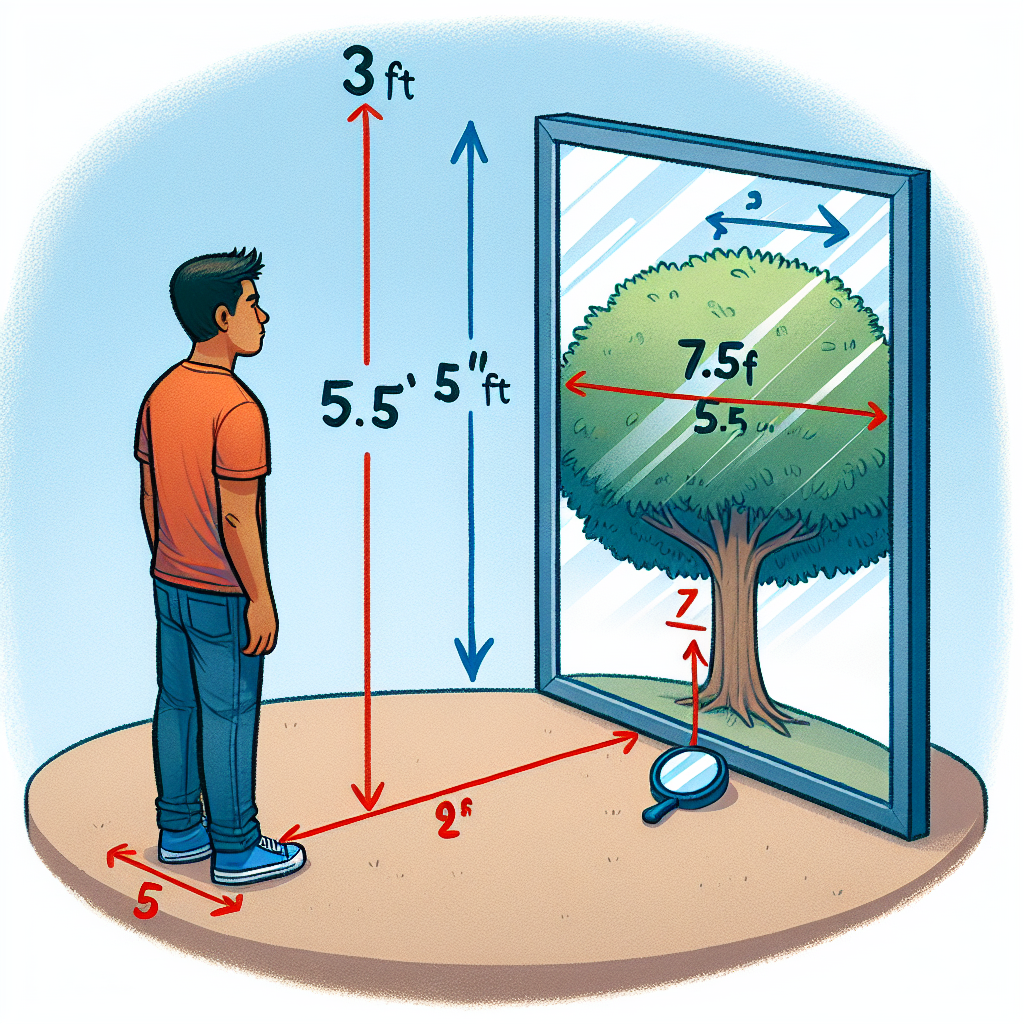
To find the height of a tree, Wyatt places a mirror so that he can see the top of the tree in the mirror. The mirror is 3 ft from him and 7.5 ft from the tree. If Wyatt is 5.5 ft tall, how tall is the tree?
How would I solve this?
Since the angle of incidence is equal to the angle of reflection in the mirror you have tow similar right-angled triangles.
Thus we can use our good ol' fashioned ratios
x/7.5 = 5.5/3
3x = 41.25
x = 13.75
or 13.8 ft to the nearest tenth of a foot
Well, to solve this problem, you can use a little bit of geometry and some imagination.
First, let's draw a diagram. Imagine that Wyatt is standing next to the tree, holding a mirror at a 45-degree angle. The mirror is 3 feet away from him and 7.5 feet away from the tree.
Now, let's use the power of imagination. Since the mirror reflects light at the same angle it hits the mirror, we can imagine that a straight line exists from the top of the tree to Wyatt's eyes. This line would hit the mirror and then bounce back up to Wyatt's eyes.
So, we have a right triangle formed by Wyatt, the mirror, and the top of the tree. Wyatt's height of 5.5 feet is the vertical leg of the triangle, and the distance between him and the mirror (3 feet) is the horizontal leg.
Now, we can use the Pythagorean theorem to find the length of the hypotenuse, which represents the height of the tree. The formula is a^2 + b^2 = c^2, where a and b are the legs of the triangle and c is the hypotenuse.
Let's plug in the numbers. We have a = 5.5 feet and b = 3 feet.
(5.5)^2 + (3)^2 = c^2
30.25 + 9 = c^2
39.25 = c^2
Now, take the square root of both sides to find the value of c:
c = √39.25
c ≈ 6.26 feet
So, the approximate height of the tree is 6.26 feet.
Just remember that this method assumes Wyatt and the tree are standing on level ground and there are no other factors affecting the measurements. Happy tree-gazing!
To solve this problem, you can use similar triangles. The ratio of corresponding sides in similar triangles is proportional.
Let's represent the height of the tree as 'h'. Since Wyatt's height is given as 5.5 ft, we have the following relationship:
(height of Wyatt) / (distance between Wyatt and the mirror) = (height of tree) / (distance between the mirror and the tree)
Substituting the given values into the equation, we have:
5.5 ft / 3 ft = h / 7.5 ft
Cross-multiplying, we get:
5.5 ft * 7.5 ft = 3 ft * h
Simplifying the equation, we have:
41.25 ft = 3 ft * h
Now we can solve for 'h' by dividing both sides of the equation by 3 ft:
41.25 ft / 3 ft = h
Therefore, the height of the tree is approximately 13.75 ft.
To solve this problem, we can use the concept of similar triangles. Similar triangles are triangles that have the same shape but might be different in size.
Let's set up a diagram to represent the situation:
Wyatt: /
|
/
/
/\
/ \
/ \
/ \
/ (tree)
/
In this diagram, let's assume that the top of the tree is point A, the bottom of the tree is point B, and the point where the mirror touches the ground is point C.
We know that point C is 3 ft away from Wyatt, point A is 7.5 ft away from C, and Wyatt's height is 5.5 ft.
To solve for the height of the tree (AB), we can create similar triangles: triangle ABC and triangle ADB, where D is the point directly below Wyatt's eye.
Using the concept of similar triangles, we can set up the following proportion:
AB/AD = BC/AC
AB/5.5 = 7.5/3
Now, we can solve for AB:
AB = (5.5 * 7.5) / 3
AB ≈ 13.75 ft
Therefore, the height of the tree is approximately 13.75 ft.
For this you have to set up a ratio of:
3/7.5=5/x
you then cross multiply 3 with x and 7.5 with 5 which gives you
3x=37.5
then divide by 3
x=12.5 ft or 12 ft 6in