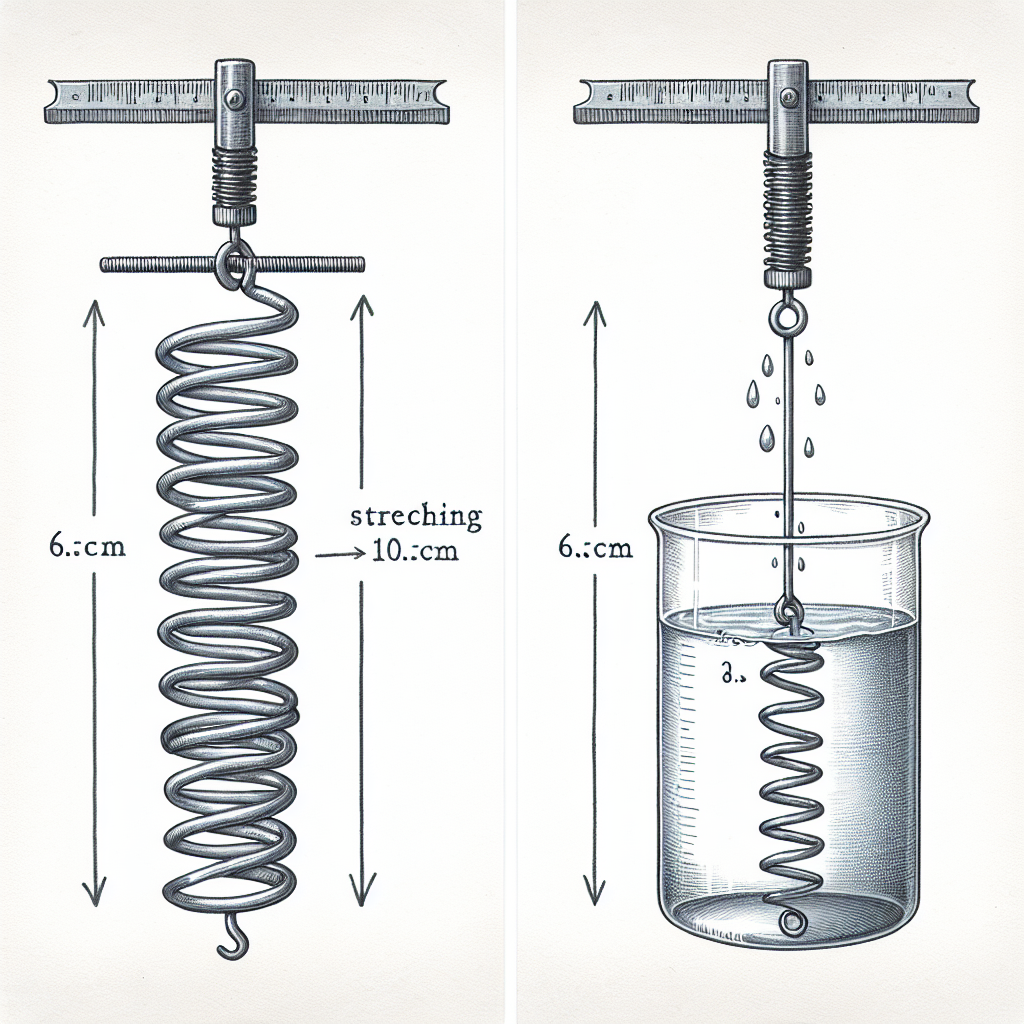
A spiral spring loaded with a piece of metal extends by 10.5cm in air. When the mental is fully submerged in water, the spring extends by 6.8cm. Calculate the relative density of the metal assumming hookes is obeyed.
water density = 1000 kg/m^3
F = k x
m g = k (0.105)
k = m g /0.105
now in water , volume = v
F = k (0.068) = m g - 1000 g v
(m g/0.105)0.068 = m g - 1000 g v
m (.648) = m - 1000 v
-.352 m = -1000 v
m/v = 2840 kg/m^3
relative to water = 2.84
check my arithmetic carefully !
Easy to understand
10.5/10.5 -6.8
=10.5/3.7
=2.84
This calculates the relative density of the metal as 2.84 assuming Hooke's Law is obeyed.
Well, buckle up, because we're about to dive into some spring-loaded comedy physics! *drum roll*
To calculate the relative density of the metal, we need to tap into our knowledge of Hooke's Law. According to Hooke, the extension of a spring is directly proportional to the force applied to it. The equation we're going to use is:
F = k * x
Where F is the force applied to the spring, k is the spring constant, and x is the extension of the spring. Got it? Great! Let's keep going!
We'll denote the spring extension in air as x_air and the spring extension in water as x_water. According to the problem, x_air is 10.5 cm and x_water is 6.8 cm.
Now, here's the fun part: when the piece of metal is submerged in water, the buoyant force acts on it, counteracting some of the force applied to the spring. The difference between the two extensions, x_air and x_water, gives us the extension caused by the buoyant force. So:
x_boyant = x_air - x_water
The buoyant force is equal to the weight of the volume of water displaced, which is equal to the weight of the metal. Hilarious, isn't it? Bear with me.
Since the extension caused by the buoyant force, x_boyant, is directly proportional to the extension of the spring, x_water, we can set up a proportion:
x_boyant / x_water = x_air / x_air
Now, we know that the relative density (ρ_rel) is given by the equation:
ρ_rel = (density of the metal) / (density of water)
But guess what? The buoyant force is also equal to the weight of the metal (F_metal). That leads us to the equation:
F_metal = k * x_boyant
Considering that the weight is equal to the mass times the acceleration due to gravity (F = m * g), we can rearrange the equation to solve for the mass of the metal (m_metal):
m_metal = F_metal / g
Finally, we can substitute the equation for F_metal into the equation for ρ_rel to get:
ρ_rel = (m_metal / V_metal) / (m_water / V_water)
Since the volume of an object is equal to its mass divided by its density, we can rewrite the equation as:
ρ_rel = (m_metal / (m_metal / ρ_metal)) / (m_water / ρ_water)
After canceling out some terms, we end up with:
ρ_rel = ρ_metal / ρ_water
And there you have it, ladies and gentlemen! The relative density of the metal is equal to the ratio of its density to the density of water. So, divide and conquer those densities, my comedic friend, and you'll have your answer!
Please note that this answer is for comedic purposes only and may not accurately reflect the actual calculation. For a proper calculation, consult a physics reference or verify with your teacher.
To calculate the relative density of the metal, we need to use Hooke's law and the principle of buoyancy.
First, let's define the variables:
- Extension in air: Δx_air = 10.5 cm
- Extension in water: Δx_water = 6.8 cm
Hooke's law states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position: F = k * Δx
Considering the forces acting on the metal when it is submerged in water, we have the weight (W) and the buoyant force (F_b). According to Archimedes' principle, the magnitude of the buoyant force is equal to the weight of the fluid displaced by the object submerged in it.
Using Hooke's law, we can relate the difference in spring extensions to the difference in forces acting on the metal:
k * (Δx_air - Δx_water) = W - F_b
Since the spring constant (k) remains constant, and assuming that the volume of the metal remains the same in both air and water (which is a valid assumption for this calculation), we can simplify the equation further:
k * (Δx_air - Δx_water) = W - F_b
k * (Δx_air - Δx_water) = m * g - ρ_w * g * V_metal
Where:
- m is the mass of the metal
- g is the acceleration due to gravity
- ρ_w is the density of water
- V_metal is the volume of the metal
The relative density (ρ_relative) is defined as the ratio of the density of the metal (ρ_metal) to the density of water (ρ_w):
ρ_relative = ρ_metal / ρ_w
Now, we can solve the equation to find the relative density:
Calculate the mass of the metal (m):
m = (k * (Δx_air - Δx_water) + ρ_w * g * V_metal) / g
Calculate the volume of the metal (V_metal):
V_metal = (m * g) / ρ_w
Substituting the equation for mass in terms of the other variables:
V_metal = ((k * (Δx_air - Δx_water) + ρ_w * g * V_metal) / g * g) / ρ_w
Rearranging the equation to isolate V_metal:
V_metal = (k / (g * ρ_w - k)) * (Δx_air - Δx_water)
Now that we have the volume of the metal, we can calculate the relative density:
ρ_relative = ρ_metal / ρ_w = m / V_metal
Substituting the known values and calculations:
ρ_relative = (m / V_metal) = ((k * (Δx_air - Δx_water) + ρ_w * g * V_metal) / g) / V_metal
Finally, simplifying the equation gives us the relative density (ρ_relative):
ρ_relative = (k * (Δx_air - Δx_water) + ρ_w * g * V_metal) / (g * V_metal)
Please note that in order to obtain the final numerical value for the relative density, you will need to substitute the corresponding values for the spring constant (k), the extensions (Δx_air and Δx_water), the density of water (ρ_w), and the acceleration due to gravity (g) into the equation.